A metodologia de modelagem de sólidos é fundamental para diversas aplicações em engenharia, requerendo por exemplo, de conceitos como distinção entre dentro e fora de uma representação 3D de um determinado objeto, para que se possa obter o seu volume e as suas propriedades de massa.

Hoje, com a evolução desses métodos, podemos citar inúmeras outras aplicações, como simular mecanismos físicos, verificar a interferência em montagens mecânicas, fazer análises de elementos-finitos, simular e controlar a fabricação em máquinas de comando numérico através do sistema CAD/CAM e muitas outras.

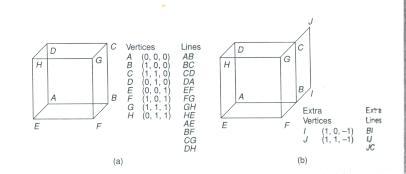
Entretanto, assim como linhas e curvas em 2D não necessariamente descrevem uma área fechada, uma coleção de planos e faces em 3D, como podemos ver na figura 1-b, não necessariamente define um volume fechado. Portanto, métodos de modelagem de sólidos nada mais são do que algorítmos capazes de criar e validar representações feitas em 3D como sendo sólidos que possam ter desejadas propriedades físicas.

Fig. 1 – (a) Um cubo em wireframe composto de 12 linhas. (b) Um cubo em wireframe com uma face extra.

Neste trabalho, discutiremos alguns dos métodos de representação mais usados hoje em dia, com ênfase em fornecer detalhes suficientes para a compreensão de como estas representações interagem com os softwares gráficos.

Consiste em formar objetos através da combinação de outros objetos com os operadores booleanos UNIÃO, DIFERENÇA e INTERSEÇÃO. Entretanto, aplicar operações booleanas ordinárias entre duas representações de sólidos pode não gerar uma outra representação válida como sólido, como podemos ver nos casos (b), (c) e (d) da figura 2

.

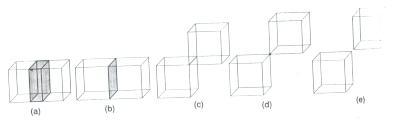
Fig. 2 - Interseção ordinária entre dois cubos pode gerar (a) um sólido, (b) um plano, (c) uma linha, (d) um ponto, ou (e) vazio.

Para solucionar o problema, foi criado o conceito de OPERAÇÕES BOOLEANAS REGULARIZADAS, cuja notação SERÁ dada por È *, Ç * e -*. Porém, antes de definir o funcionamento dessas operações, vamos entender um outro conceito importante que é OBJETO REGULARIZADO.

Um objeto qualquer, pode ser definido como um conjunto de pontos divididos em pontos do interior e pontos do contorno. Pontos do contorno são aqueles cuja distância entre objeto e o seu complemento é zero, enquanto pontos do interior são todos os outros pontos. Um objeto regularizado é definido como o fechamento (closure) do conjunto de pontos interiores como podemos ver na figura 3.

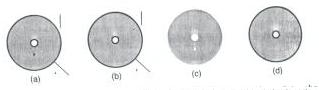
Fig. 3 - Regularizando um objeto. (a) Objeto qualquer é definido pelos pontos do interior (em cinza), pontos de contorno que fazem parte do objeto (em preto) e outros pontos (em cinza escuro). (b) Fechamento do objeto: todos os pontos de contorno passam a fazer parte do objeto. (c) Interior do objeto: retira-se todos os pontos de contorno. (d) Regularização do objeto é o fechamento de seu interior.

Portanto, a definição de cada operação booleana regularizada, em termos da ordinária correspondente , pode ser dada como

A op* B = closure(interior(A op B))

Onde op é um dos operadores È , Ç ou - . Consequentemente, operadores booleanos regularizados produzem objetos regularizados quando aplicados a outros dois objetos regularizados.

A figura 4 mostra, por exemplo, uma comparação de uma operação de interseção ordinária com uma regularizada aplicada nos objetos (a), na posição (b).

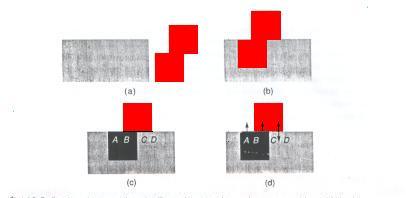
Fig. 4 - Interseção booleana. (a) Dois objetos mostrados em corte. (b) Posição em que os objetos serão interceptados. (c) Interseção ordinária resulta em uma face flutuante, representada pelo segmento CD. (d) Interseção regularizada inclui o segmento AB resultante do contorno de ambos objetos porque eles estão do mesmo lado, isto é, a normal de ambos têm o mesmo sentido, e exclui o segmento CD por estarem em lados opostos. Interseções de contornos e interiores são sempre incluidos BC.

O resultado de cada operador regularizado, pode ser definido em termos dos operadores ordinários aplicados a contornos e interiores de objetos. A tabela a seguir, mostra como os operadores regularizados são definidos para quaisquer objetos A e B.

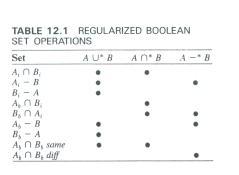
A figura 5, mostra o resultado das operações que aparecem na tabela, sendo que os índices "b" e "i" das notações indicam respectivamente contorno e interior dos objetos. A_b Ç B_b same é a interseção do contorno de A e B em que A_i e B_i estão do mesmo lado, e A_b Ç B_b diff quando A_i e B_i estão em lados opostos.

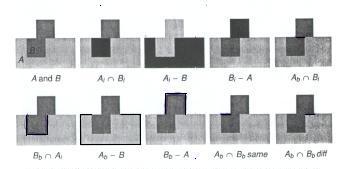
Fig. 5 – Operações booleanos ordinárias aplicados nos objetos A e B.

Portanto, cada operação regularizada é definida pela união dos resultados de cada operação ordinária marcada com · em cada coluna da tabela apresentada anteriormente.

Neste caso, primitivas simples são combinadas através de operadores booleanos regularizados que são incluídos diretamente na representação. O objeto é então armazenado como uma árvore de operadores (nós) e primitivas simples Fig. 6.

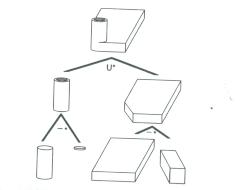
Fig. 6 – Um objeto definido por CSG e sua árvore.

Alguns nós representam operadores booleanos, e outros representam translação, rotação, escala e etc.

Em algumas implementações, as primitivas são sólidos simples, como cubos ou esferas, em outros sistemas, primitivas são combinadas com "half-spaces", que apesar de não ser considerado um sólido fechado, simplificam a representação de certas estruturas, pois funcionam, por exemplo, como planos de cortes.

Apesar de não ser ambígua, CSG não provê uma representação única. Isto é, podemos ter mais de uma representação para um mesmo objeto resultante (figura 7).

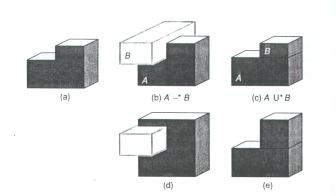
Fig. 7 – O objeto mostrado em (a) pode ser definido por diferentes operações CSG (b) e (c). Aumentando a altura da face mais alta em (b) e (c), obtemos diferentes objetos mostrados em (d) e (e).

Em primitive instancing, o sistema de modelagem é definido por um conjunto de primitivas (sólidos 3D) que são relevantes para uma determinada área de aplicação. Essas primitivas são tipicamente parametrizadas em termos de transformações e propriedades. Primitive instancing é muitas vezes usada para objetos relativamente complexos, como engrenagens (figura 8), parafusos ou outros que pertençam a um mesmo grupo tecnológico, onde dentro de uma gama de parâmetros, pode-se obter uma variedade de representações de objetos através da variação de apenas alguns desses parâmetros.

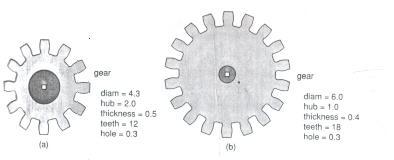
Fig. 8 – Duas engrenagens definidas por primitive instancing

.

Consiste em percorrer um objeto 2D (área) ao longo de uma trajetória através do espaço para se definir um novo objeto (3D). De acordo com o processo, o sweep pode ser divido em três grupos. TRANSLAÇÃO, quando a trajetória é normal a área (2D). Neste caso, o volume pode ser obtido facilmente pela produto da área pelo comprimento percorrido. ROTAÇÃO, obtido pela rotação da área em torno de um eixo. GENÉRICOS, são aqueles em que a área ou volume variam em tamanho, forma ou orientação de uma trajetória curva arbitrária.

Fig. 9 – Sweepes. (a) 2D áreas são usadas para definir (b) sweeps transladados e (c) sweepes rotacionados.

Como podemos ver na figura 10, simples sweeps não são compatíveis com operações booleanas regularizadas.

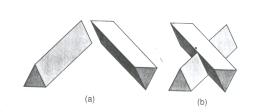
Fig. 10 – (a) 2 sweepes simples de objetos 2D (triangulos). (b) União dos sweepes mostrados em (a) não pode ser obtido através do sweep de um objeto (2D).

Em Spatial-Partitioning representations, um sólido é decomposto numa coleção de sólidos mais primitivos que o sólido original. Essas primitivas podem variar em tipo, tamanho, posição, parametrização e orientação. A forma de representação que objetivamos apresentar é a Octrees, mas antes vamos entender outras formas mais simples.

Cell Decomposition é uma das formas mais genéricas, onde cada sistema de decomposição celular define um conjunto de células primitivas que são tipicamente parametrizadas. Na verdade, é como se fosse uma mistura de Primitive Instance e CSG, mas que difere por podermos compor objetos mais complexos a partir de outros mais simples, o que não ocorre na Primitive Instance, e basicamente utilizar apenas a operação de união regularizada, o que não ocorre no caso da CSG. Portanto, como podemos ver na figura 11, assim como na representação CSG, Cell Decomposition não é ambígua e nem necessariamente única.

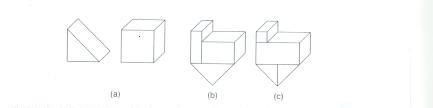
Fig. 11 – Os objetos mostrados em (a), podem ser transformados para a construção de um mesmo objeto mostrado em (b) e (c) por diferentes arranjos.

Concluindo, apesar de Cell Decomposition ser uma representação de difícil validação, ela é muito importante para análise de elementos finitos.

Spatial-Occupancy Enumeration é um caso particular de Cell Decomposition, em que o sólido é decomposto em um arranjo de células idênticas em um GRID fixo e regular. Muitas vezes essas células são chamadas de voxels (elementos de volume) em analogia aos pixels. O tipo de célula mais comum é o cubo, e um vetor de cubos regulares é chamado de cuberille (figura 12). O controle de uma representação é feito pela presença ou ausência de uma célula simples em cada posição do grid, o que resulta numa forma única e não ambígua de representação.

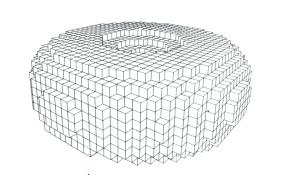
Fig. 12 – Torus representado por Spatial-Occupancy Enumeration

Spatial-Occupancy Enumeration é muito usado em aplicações biomédicas, como tomografia computadorizada.

Como também podemos ver na figura 12, em muitos casos, o sólido pode ser apenas uma aproximação de suas dimensões reais, pois uma representação exata depende do tipo de células e do sólido em questão.

Octrees e Quadtrees são variações hierarquica de Spatial_Occupancy Enumeration. O Quadtree é uma forma de representação usado para reproduzir imagens 2D, e o Octree foi derivado de Quadtree para imagens 3D.

A idéia fundamental de ambos Quadtree e Octree é a divisão estruturada de uma subdivisão binária. Um Quadtree é obtido através de sucessivas subdivisões de duas dimensões num plano 2D para formar quadrantes, como mostra a figura 13.

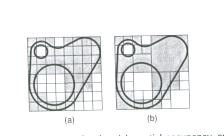
Fig. 13 – Um objeto representado usando (a) Spatial-Occupancy Enumeration (b) Quadtree.

Quando um Quadtree é usado para representar uma área num plano, cada quadrante pode estar completo, parcialmente preenchido ou vazio, representados na figura 14 pelas letras F, P e E por causa do inglês Full, Partially Full e Empty. Um quadrante parcialmente preenchido é recursivamente subdividido até que todos os quadrantes fiquem homogêneos (completo ou vazio) ou até que um nível predeterminado de divisão é alcançado. As sucessivas subdivisões podem ser representadas por uma árvore com os quadrantes parcialmente preenchidos nos nós internos e os completos e vazios nas extremidades.

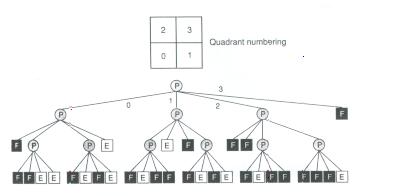
Fig. – 14 - Estrutura de dados em Quadtree para o objeto da figura 13 (b). F = full, P = partially full, E = empty

O Octree é similar ao Quadtree, com exceção de que envolve 3 dimensões recursivamente subdivididas em octantes (figura 15).

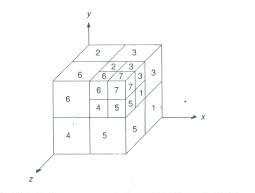
Fig. 15 – Octree enumeration. Octante 0 não é visível.

Uma grande vantagem das representações Quadtrees e Octrees, como vamos ver a seguir, é a facilidade de manipulação dos dados armazenados. Isto é, algorítmos para operações booleanas, transformações e localização de nós adjacentes.

Tem-se trabalhado muito no desenvolvimento de algorítmos eficientes para armazenar e processar Quadtrees e Octrees. Como exemplo, vamos analisar os procedimentos dos algorítimos das operações booleanas União e Interseção das duas árvores de representação em Quadtrees, já que analogamente é o mesmo para Octrees, dos objetos S e T, mostrados na figura 16 (a) e (b)

Em ambos os casos, União e Interseção, os nós são examinados de cima para baixo, par a par e em seus respectivos níveis, sendo que o resultado é obtido conforme o seguinte procedimento:

1 – Se um dos nós for preto, o nó resultante será preto.

2 – Se um dos nós for branco, o nó resultante assume o valor do outro, isto é, o que não é branco.

3 – Se ambos forem cinza, o nó resultante será cinza.

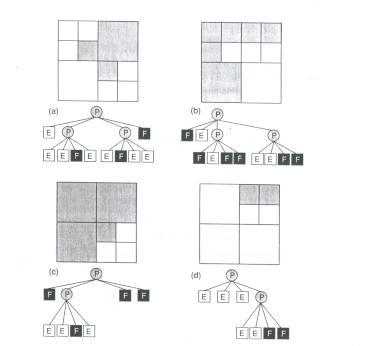
Fig. 16 – Operações Booleanas em Quadtree. (a) Objeto S em Quadtree. (b) Objeto T em Quadtree. (c) S È T. (d) S Ç T.

O algorítmo é aplicado recursivamente até os pares do último nível, sendo que o último nível da arvore resultante deve ser inspecionado, pois se um conjunto de nós de um mesmo quadrante for todo preto, estes serão apagados e o nó correspondente de ordem superior é trocado de cinza para preto.

1 – Se um dos nós for branco, o nó resultante será branco.

2 – Se um dos nós for preto, o nó resultante assume o valor do outro, isto é, o que não é preto.

3 – Se ambos forem cinza, o nó resultante será cinza.

Novamente, o algorítmo é aplicado recursivamente até os pares do último nível e o último nível da arvore resultante também deve ser inspecionado, porém, neste caso, se um conjunto de nós de um mesmo quadrante for todo branco, estes serão apagados e o nó correspondente de ordem superior é trocado de cinza para branco.

Portanto, podemos observar que os algorítimos União e Interseção são similare, exceto que os valores preto e branco ficam trocados.

Além das operações booleanas, em Octrees e Quadtrees é muito fácil aplicar transformações simples como rotação por múltiplos de 90º, escalas de dobro e metade, e reflexões. Entretanto, translações e outras transformações mais genéricas são mais complexas.

Uma operação importante em Quadtrees e Octrees é a localização de um nó vizinho (adjacente) a um certo nó original. Primeiramente, é importante observarmos que um nó Quadtree tem 8 direções possíveis de vizinhança. Isto é, 4 vizinhos na direção dos lados (N,S,E e W) e 4 na direção dos vértices (NW,NE,SW e SE). Já um nó Octree, tem 26 direções possíveis: 6 ao longo das faces, 12 ao longo dos lados e 8 ao longo dos vértices.

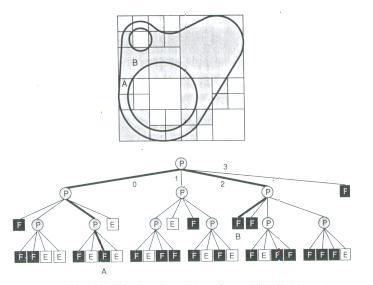
Fig. 17 – Localização de nós adjacentes em Quadtree.

Descreveremos aqui, o exemplo da figura 17, onde se deseja obter o vizinho N do nó A, isto é, o nó B. Portanto, começando em A, a sequência de escalada nos níveis é a seguinte: NW -> NW -> SW , parando quando se encontra um nó S. Para obter a sequência de descida nos níveis, faz-se uma reflexão em torno do eixo N-S e obtem-se: NW -> SW.

Como vimos, Modelagem de Sólidos é importante tanto para sistemas CAD/CAM quanto para gráficos em geral. Entretanto, embora já existam muitos algorítmos e sistemas sendo largamente utilizados, ainda restam muitos problemas de difícil solução para serem resolvidos.

· J. D. Foley, A. van Dam, S.K.Feiner, J.F.Hughes. Computer Graphics – Principles and Practice.