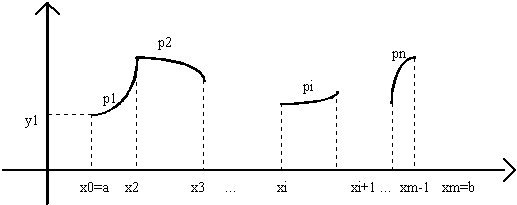
texto de Tereza Godim

Interpolação Spline

É uma técnica de aproximação que consiste em se dividir o intervalo de interesse em vários subintervalos e interpolar, da forma mais suave possível, nestes subintervalos com polinômios de grau pequeno.

Definição. Sejam uma subdivisão do intervalo [a,b]. Uma função spline de grau p com nós nos pontos (xi ,fi)(i=0,m) é uma função sp(x) com as propriedades:

a) em cada subintervalo [xi,xi+1] (i=0,m-1), sp(x) é um polinômio de grau p.

b) sp(x) é contínuo em [a,b] e tem derivada contínua em [a,b] até ordem p.

A spline interpolante é a função sp(x) tal que sp(xi)=f(xi) (i=0,m).

Splines, usadas em desenhos de engenharia, são réguas flexíveis, de madeira ou plástico, que podem ser curvadas de forma a passar por um dado conjunto de pontos (xi,fi) chamados nós. Apesar de ser usada desde o século passado, só no fim da década de 60 foi desenvolvida a formulação matemática deste problema. Tal formalização possibilitou o desenvolvimento de vários sistemas computadorizados que utilizam aproximações gráficas de funções como CAD/CAM e TURBO GRAFIX.

Obs: Ducks são pesos que são fixados nas áreas de interesse causando a deformação da estrutura de madeira ou plástico resultando assim na curva.

M(x) = EI / R(x) (Equação de Euler para o momento de defletor)

E – cte determinada pelo material da estrutura física.

R(x) - raio de curvatura.

I - é o momento de inércia.

Para pequenas deflecções o raio de curvatura é equivalente a y’’ ou seja:

1/R(x) = y’’

donde:

y’’=M(x)/EI

Assumindo que os pesos variem linearmente entre os suportes o momento deflector fica:

M(x)=Ax+B

Substituindo na equação de Euler:

EI

Aplicando – se a integral dupla temos

y=A₁x³ + B₁x² + C₁x + D₁

A spline física é descrita matemáticamente através de um polinômio cubico.

Em geral, o spline matemático é um polinômio de grau K com continuidade de derivada de ordem K-1 nas juntas comuns entre segmentos. Assim, o spline cúbico tem segunda-ordem ou continuidade de C² nas juntas. Splines de polinômios de baixo-grau são muito úteis para curva que ajusta polinômios de baixo-grau reduzem as exigências computacionais e também reduzem instabilidades numéricas que causam oscilações indesejáveis quando são unidos vários pontos em uma curva comum. Porém, desde que polinômios de baixo-grau não podem medir uma série arbitrária de pontos, segmento de polinômios adjacente é usado. Baseado nestas considerações e fazendo analogia com o spline físico, uma técnica comum é usar uma série de segmentos splines cúbicos com cada segmento di vidindo somente dois pontos. Alem disso, o spline cúbico é vantajoso desde que a curva de mais baixo grau que permite um ponto de inflexão e a qual tem a habilidade para torcer sobre o espaço.

A equação para um único segmento de spline cúbico paramétrico é determinada por

P(t)= S ⁴_i=1BiT^i-1 t1<=t<=t2 (5-1)

onde t1 e t2 são valores de parâmetro que iniciam e finalizam o segmento. P(t) é o vetor de posição de qualquer ponto no segmento de spline cúbico. P(t)=[x(t) y(t) z(t)] é o valor vetorial da função .

Os três componentes de P(t) é as coordenadas Cartesianas do vetor posição. Cada componente tem uma formulação semelhante a P(t), i.e.,

x(t)= S ⁴_i=1B_ixT^i-1 t1<=t<=t2 (5-1)

y(t)= S ⁴_i=1B_iyT^i-1 t1<=t<=t2 (5-1)

z(t)= S ⁴_i=1B_izT^i-1 t1<=t<=t2 (5-1)

Os coeficientes constantes Bi são determinados especificando quatro condições de fronteira para o segmento spline. Transcrevendo a Eq. (5-1) produz:

P(t)=B₁+B₂t+B₃t²+B₄t³ t1<=t<=t2 (5-2).

Seja p1 e P2 os vetores posição no fim do segmento da spline. Também seja P'1 e P' 2, os derivado com respeito a t, ser os vetores tangentes aos fins do segmento de spline.

Diferenciando a Eq.(5-1) produz:

P’(t)=[x’(t) y’(t) z’(t)] = S ⁴_i=1B_i (i-1)t^i-2 t1<=t<=t2 (5-3)

Transcrevendo este resultado obtemos:

P’(t)=B₂+2B₃t+3B₄t² t1<=t<=t2 (5-4)

Assumindo, sem perda de generalidade, que t1=0 e aplicando o quatro condições de fronteira,

P ( 0) = P₁ (5-5a)

P (t2) = P₂ (5-5b)

P’( 0) = P₁’ (5-5c)

P’(t2) = P₂’ (5-5d)

Produz quatro equações para o Bi desconhecido. Especificamente,

P(0)=B1=P1

P’(0)= S ⁴_i=1 (i-1)t^i-2 Bi |_t=0 = B2 = P’1

P(t2)= S ⁴_i=1 Bi t^i-1 |_t=t2 =B₁ + B₂t₂ + B₃t²₂+B₄t³₂

P’(t2)= S ⁴_i=1 (i-1)t^i-2 Bi |_t=t2 = B2 + 2B₃t₂+3B₄t²₂

Resolvendo para B3 e B4 produz:

B3 = 3(P₂-P₁)/t₂² - 2P’₁/t₂ - P’₂/t₂ (5 - 7a)

e

B4 = 2(P₁-P₂)/t₂³ - P’₁/t₂² - P’₂/t₂² (5 – 7b)

Estes valores de B1, B2, B3 e B4 determinam o segmento de spline cúbico.

Note que a forma do segmento depende da posição dos vetores tangentes no final do segmento.

Além disso, note que o valor do t=t2 de parâmetro ao término do segmento aparece nos resultados.

Considerando que cada da posição finais e vetores tangentes tem três componentes, a equação paramétrica para uma curva espacial cúbica depende de doze componentes vetoriais e o valor do parâmetro t2 ao término do segmento.

Substituindo nas Eq. (5-6) e (5-7) na Eq. (5-1) obtemos a equação para um único segmento de spline cúbico:

P(t)= P₁ + P’₁t + [3(P₂-P₁)/t₂² - 2P’₁/t₂ - P’₂/t₂ ] t²

+[2(P₁-P₂)/t₂³ - P’₁/t₂² - P’₂/t₂²] t³ (5-8)

Equação (5-8) é para um único segmento de spline cúbico. Porém, para representar uma curva completa, são unidos segmentos múltiplos. Contanto que os vetores de posição P1,P2,P3, os vetores tangentes P'1,P'2,P'3 e os valores dos parâmetros t2, t3 são conhecidos, então a Eq.(5-8),aplicada para cada dois segmentos, suas formas. Porém, é improvável que o vetor tangente P'2 na junta interna entre os dois segmentos é conhecido.

Felizmente, o vetor tangente interno que P'2 pode ser determinado impondo uma condição de continuidade na junta interna.

Relembrando que uma spline de grau K tem continuidade de ordem K-1 nas juntas internas.

Assim, um spline cúbico tem continuidade de segunda-ordem nas juntas internas. Isto significa que o Segunda derivada P''2(t) é contínua ao longo da junta; i.e., a curvatura é contínua ao longo junta. Diferenciando a Eq.(5-1) duas vezes obtemos:

P''= S ⁴_i=1 (i-1) (i-2) Bi t^i-3 t1<=t<=t2

Note que para o primeiro segmento spline cúbico a região 0<=t<=t2,avaliando a Eq. (5-9) no final do segmento onde t=t2 obtemos:

P''=6B₄t₂+2B₃

Durante o segundo segmento spline cúbico a região é 0<=t<=t3. Avaliando. A Eq.(5-9) do começo deste segundo segmento onde t=0 obtemos:

P''=2B₃

Comparando estes dois resultados e usando Eqs. (5-6a,b) e (5-7a) obtemos:

6t₂ [ 2 ( P₁ – P₂ )/t₂³+ P’₁ /t₂²- P’₂ /t₂²] + 2 [ 3(P₂ – P₁)/t₂² – 2P’₁ /t₂– P’₂ /t₂]

Aqui o lado à esquerda da equação representa a curvatura do fim do primeiro segmento e o lado à direita a curvatura no começo do segundo segmento. Multiplicando por t2t3 e juntando os termos dados

t₃P’₁ + 2(t₃ + t₂ ) P’₂ + t₂ P’₃ = 3 [ t₂( P₃ – P₂) = t₂ (P₂ – P₁)] ( 5 – 10)

que pode ser resolvido para P'₂, o vetor tangente desconhecido na junta interna.

Novamente note que o valor final de t,i.e, t₂ e t₃, aparecem na equação resultante.